第十五讲 从赌博到认识世界——概率统计三大招

在香港，上世纪九十年代的影坛，有一系列非常精彩的电影《赌神》《赌圣》《赌侠》，向大众展现了一个个虚构的世界，骰子抛得让人眼花缭乱，扑克牌在手上可以随意变化。这样的赌术，这样的牌技，真的存在吗？他们背后除了老千和魔术手法，有数学上的依据吗？

我们平时见到的世界，发生的事情很多是确定的，比如，2-1=1，本来有两块骨头，吃掉了一块肯定还剩下一块。但是，有些事情却是无法预料的。比如，扔一枚硬币，你无法预测它掉下来后，是正面朝上，还是反面朝上。扔一颗没有机关和猫腻的正常骰子，你也无法预知出来的，是1到6点中的哪一个。这些事件，代表了世界的不确定性，和随机性。

最早研究这种不确定性的，是意大利文艺复兴时期的学者卡尔达诺。

他是个医学博士，以行医为业，业余时间研究哲学、数学、物理、占星算卦，还有就是赌术，而且还靠赌术赚了不少钱。

他在1545年出版了《大术》一书，里面有一元三次方程的解法，后人称为卡尔达诺公式，也称卡当公式。实际上，后来的史学家发现，这是他从另一位数学家塔塔利亚那里骗来的。书中还记载了一元四次方程的解法，是由他的学生费拉里发现的。

他的死法也颇为奇葩。因为他占星算命的名气比较大，是宫廷御用首席占星大师。骨骼清奇的他，在71岁时通过占星术推算出，自己将在四年之后，1576年9月21日去世。遗书和葬礼都安排完毕，但是到了那一天，他居然发现自己“吃好喝好身体倍儿棒”。为了保全自己算命大师的名声，他只好自杀了。

卡尔达诺死后，有人把他研究赌博的书《论赌博游戏》出版发表。在书中，他第一次用数字来描述随机事件发生的可能性。比如扔硬币，正面和反面出现的可能性是相等的，概率就是1/2。扔骰子，有6种可能，每种可能的概率是1/6。概率，是一个0～1之间的数，越接近1，表示它越可能发生。概率为1，就是肯定会发生。概率为0，就是不可能发生。

这一划时代的思想对随后产生的概率论、统计学有深远影响。他也算是概率论的鼻祖、古今中外第一位赌神了。可见，最早的概率，是和赌博密不可分的。

但是，概率研究的不确定性，里面究竟有没有规律呢？

我们的大数学家雅可比•伯努利又登场了，喜欢研究“1个亿小目标”的他，怎么会放过赌博这样一夜暴富、达到小目标的事情呢？他找到了概率里面的规律，偶然中的必然性。

一枚硬币被抛出后，有50%的可能为正面或者反面。10次里可能有4次正面6次反面，也可能是7次正面3次反面，这很正常。但是，随着抛硬币的次数的增多，扔上几百次、几千次、几万次，正面和反面出现的次数，就会越来越接近于相同，各占一半。

这就是概率和统计理论里的第一个大招——大数定律。用数学的语言来描述就是，当试验次数无限增大时，事件出现的频率稳定于它出现的概率。

根据大数定律，你扔骰子，只要你扔的次数足够多，几百次、几千次、几万次，一定有两个后果出现：第一，出现1～6点的频率，越接近各占1/6。第二，你的手酸了。

大数定律以严格的数学形式，揭示了随机现象的本质之一：平均结果是稳定的。在我们的生活中处处可以看到有趣的大数定律。

有一段时间，一位人口统计学家调查发现，欧洲各地的男孩与女婴孩的出生比例是22:21。但是，在法国巴黎的比例却是25:24。他觉得很蹊跷，决心去搞个明白。最后，他发现了原因，原来当时的巴黎重女轻男，一些人会丢弃男婴。

你可以统计一下学校里男女生的比例，看看有什么异常情况？市三女中的同学就不要统计了哈。

赌场赚钱的秘诀也是在于大数定律。赌博机被设计出来赢和输的比例，并不是“50%：50%”，而是“51%:49%”的预期概率——赌场赢的概率至少51%。大家别小看这一点点偏差，赌场不会和你进行“一把赌输赢”，他们会不停地、大量地招揽赌客，然后，让大数定律发挥威力。随着赌博机转动，赌徒们以为自己要赚大钱了，最后却是赌场坐收渔利。

和伯努利同时期的法国科学家帕斯卡，和著名非专业数学家费马（费马大定理的“挖坑人”），也一起研究过赌金分配问题，对早期概率论的发展颇有影响。

概率和统计理论里的第二个大招——中心极限定理，曾经印在德国的10马克纸币上，一个像钟的形状的曲线，以及数学王子高斯的头像。这个定理是由法国的数学家棣莫弗和拉普拉斯发现的，后来由高斯在18岁时再次发现，并做了提升和推广。

我们平时做民意调查，比如

现在的中学生喜不喜欢饶舌歌？

今年高考的数学题出得是不是不好？

你相不相信有外星人存在？

你去随机找100个人做调查，然后得到一个结果，比如，76个喜欢饶舌歌。

小明也随机找另外100个人做调查，然后得到一个结果，有34个喜欢饶舌歌。

小红也随机找另外100个人做调查，然后得到一个结果，有64个喜欢饶舌歌。

学校的500位同学都去做民意调查了……

为了民意结果，大家都是拼了。

你把500个调查结果画成曲线。横坐标，是每次调查100人中喜欢饶舌歌的人数，当然是在0到100之间。纵坐标呢？是500次调查中有0个、1个、2个……100个人喜欢饶舌歌的次数。

最后，你会发现，这个曲线的形状，就是“钟形分布”。这个钟，最突起的高峰，代表了500个民意调查中出现最多的结果，比如说每100个中学生中，有66个喜欢饶舌歌曲。500次调查，大部分的结果集中在60～70中间，有少数调查结果在50～60和70～80之间，更少的在40～50和80～90之间，40以下和90以上的结果很少。

你对民意调查入了迷，决定再次发动全校同学做高考数学题的调查。

同样派500个人出去调查，每个调查员去问100人。

最后的结果太让人意想不到了，虽然高峰的位置移动了，形状变得瘦瘦窄窄了，但是，居然还是一口钟的形状。这口钟大部分的调查结果，集中在90～95中间。

这是怎么回事呢？明明是在调查不同的事情，一个是饶舌歌，一个是高考数学题，怎么形状都一样？都是这样的“钟”呢？

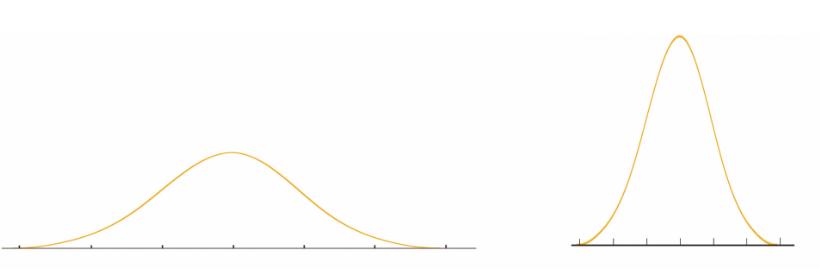
这就是数学家发现的中心极限定理：

我们每个人去做的调查，就是一个样本。不管我们要研究的总体是什么问题，高考数学题也好，流行歌曲的喜爱也好，外星人存在与否也好，我们把很多样本集中起来，得到的平均值都会围绕在总体的平均值周围，像一口“钟”一样分布，这也叫正态分布或者高斯分布。

这个中心极限是我们做统计活动、民意调查的理论依据。它让我们可以根据一些样本的结果，来推断真实世界的情况。总统的支持率，电视剧的收视率，都是这样来统计的。

概率统计里的第三个大招，叫“贝叶斯分析”。

前面我们已经能够计算“正向概率”，比如，假设袋子里面100个白球，10个黑球，你伸手进去摸一把，摸出黑球的概率是多大呢？ 10/110，对不对？

但是，如果我反过来问：如果事先并不知道袋子里面黑白球的比例，而是闭着眼睛摸出好几个球，观察这些取出来的球的颜色之后，我们能不能推测袋子里黑白球的比例？

这个问题，就是所谓的逆向概率问题，是由英国的数学家托马斯•贝叶斯提出来的。他是想从样本来推断全体，从结果去推断原因。

贝叶斯分析有着非常深刻的哲学和数学意义：现实世界本身是不确定的，人类的观察也是表面的。沿用刚才那个袋子里面取球的比方，我们往往只能知道从里面取出来的球是什么颜色，而并不能直接看到袋子里面实际的情况。这个时候，我们就需要做一个猜测。所谓猜测，当然是不确定的，但也绝对不是忽悠瞎蒙。我们需要根据贝叶斯分析，算出各种不同猜测的可能性大小，再找到最可能的判断。

大数定律，中心极限定理，贝叶斯分析，实际上是我们认识这个世界的基础。现在比较流行的“大数据”分析，背后的理论依据，也是这些概率统计的基本知识。有人说：21世纪的竞争是数据的竞争，谁掌握数据，谁就掌握未来。实际上，这句话是不完整的。真正掌握未来的，是掌握了数据和概率统计三大招的人。看到这里，你对未来是不是更有信心了？

下一回，我们要讲一种想象出来的数，它虽然不是真实的存在，却和现代科学息息相关。